Jak nerozhodný zahradník stále přesazoval… I takto by se dala nazvat následující matematická úloha. Zvládnete ji vyřešit i bez podrobné nápovědy?
Troufáte si na toto zadání? Úloha není tak složitá, jak se může někomu na první pohled zdát.
Pokud by máte pocit, že vám chybí informace, jaké rozměry má zahrada, tak je dostatečně velká, abychom keř z jeho původní pozice mohli libovolně přesazovat.
Ještě nevíte, jak přijít na správnou odpověď? Nevadí, od toho jsme tady! Postupně se proklikejte nápovědami, které vás dovedou ke správnému řešení. Příště vás už takový příklad nepřekvapí.
Nápověda 1
Zaměřte se na údaje, které vyčtete přímo ze zadání. Znáte relativní původní pozici keře a znáte vzdálenosti, o které byl přesazován a přesouván.
Nápověda 2
Celkem byl keř zasazený na 4 různých místech:
-
- původní místo,
- místo po přesunu na západ,
- místo po přesunu na sever,
- místo po přesunu na východ = finální pozice.
Zkuste to zakreslit do pomocného obrázku. Začněte od původní pozice keře – doporučujeme, ať si narýsujete na papír mřížku a keř umístěte na jeden z bodů mřížky. Můžete rovněž kreslit na čtverečkovaný papír.
My v náčrtku znázorňujeme původní pozici keře červeným křížkem.
Nápověda 3
Do rohu vašeho papíru si můžete zakreslit směrovou růžici, která vám pomůže s orientací podle světových stran. V tu chvíli pro vás přesun keře na sever znamená posun směrem nahoru v naší mřížce, to samé platí i pro další světové strany.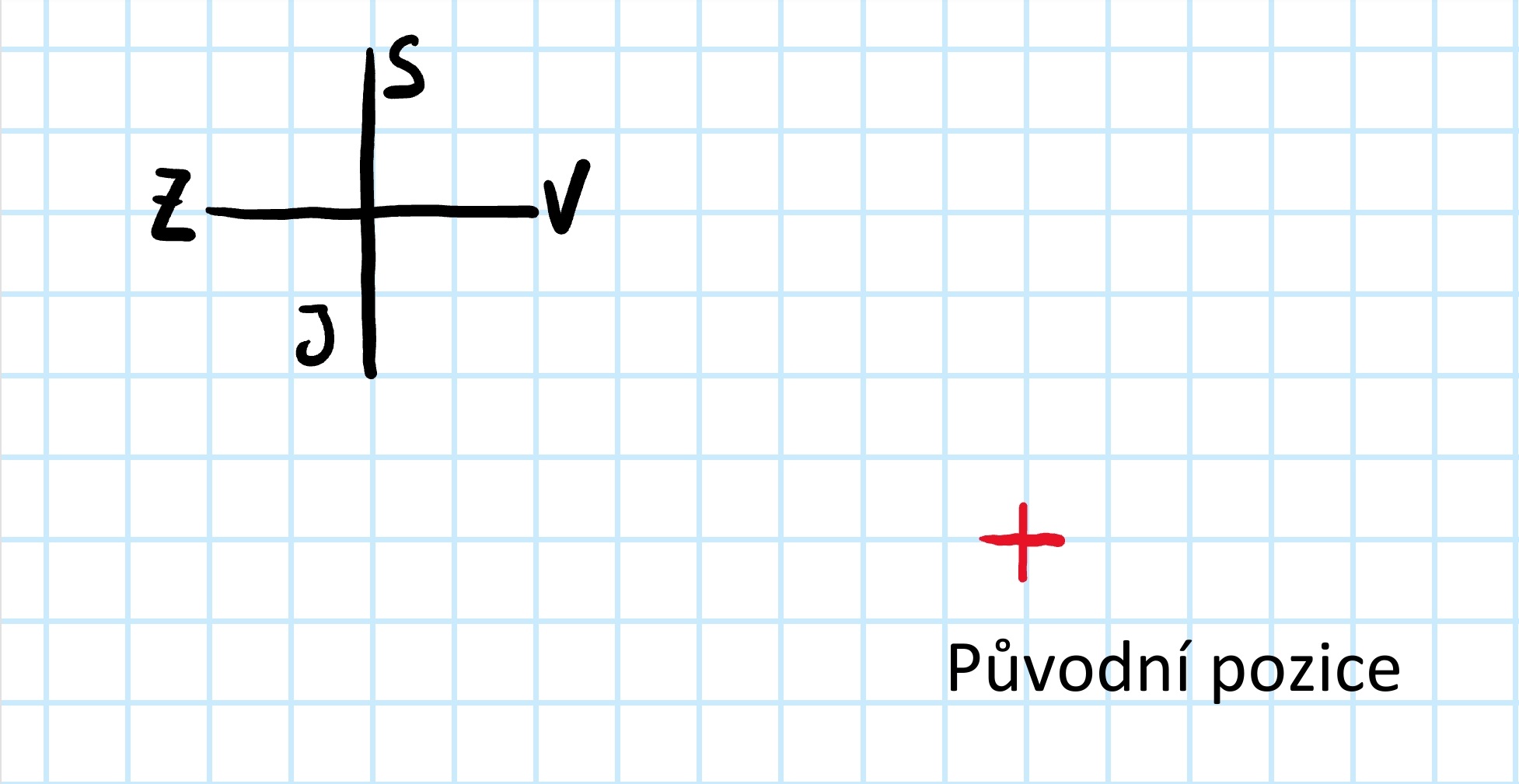
Nápověda 4
Teď už se jen pohybujete v mřížce a zaznamenáváte si přesazení keře. Jděte postupně podle zadání úlohy, nejprve tedy keř přesadíte o 2 metry na západ, což odpovídá posunu o 2 čtverce vlevo.
Posun značíme zelenými obloučky, momentální pozice keře je označena zeleným křížkem.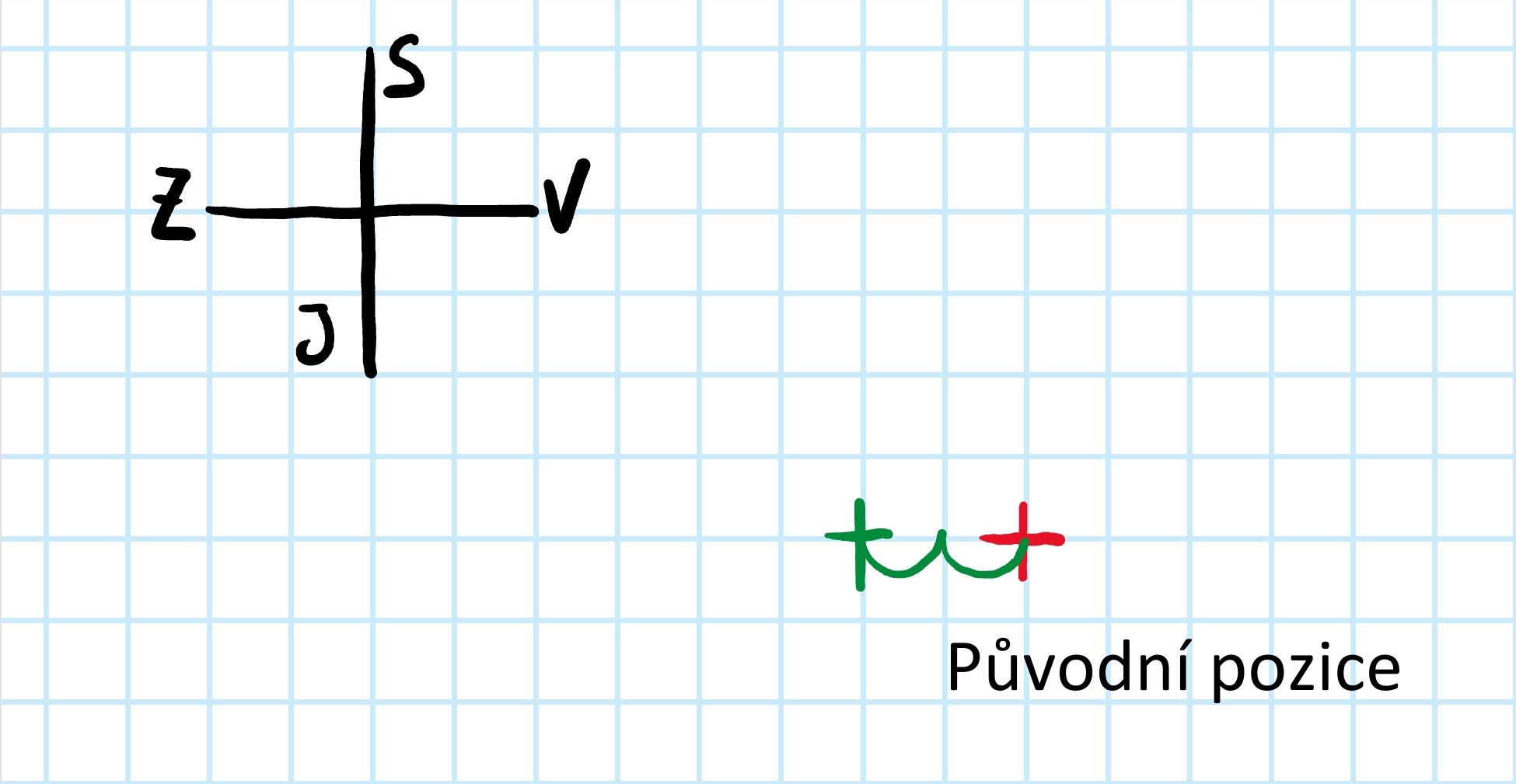
Nápověda 5
Další posun je o 4 metry na sever, 4 čtverce nahoru.
V náčrtku je posun znázorněn oranžovými obloučky, momentální pozice keře oranžovým křížkem.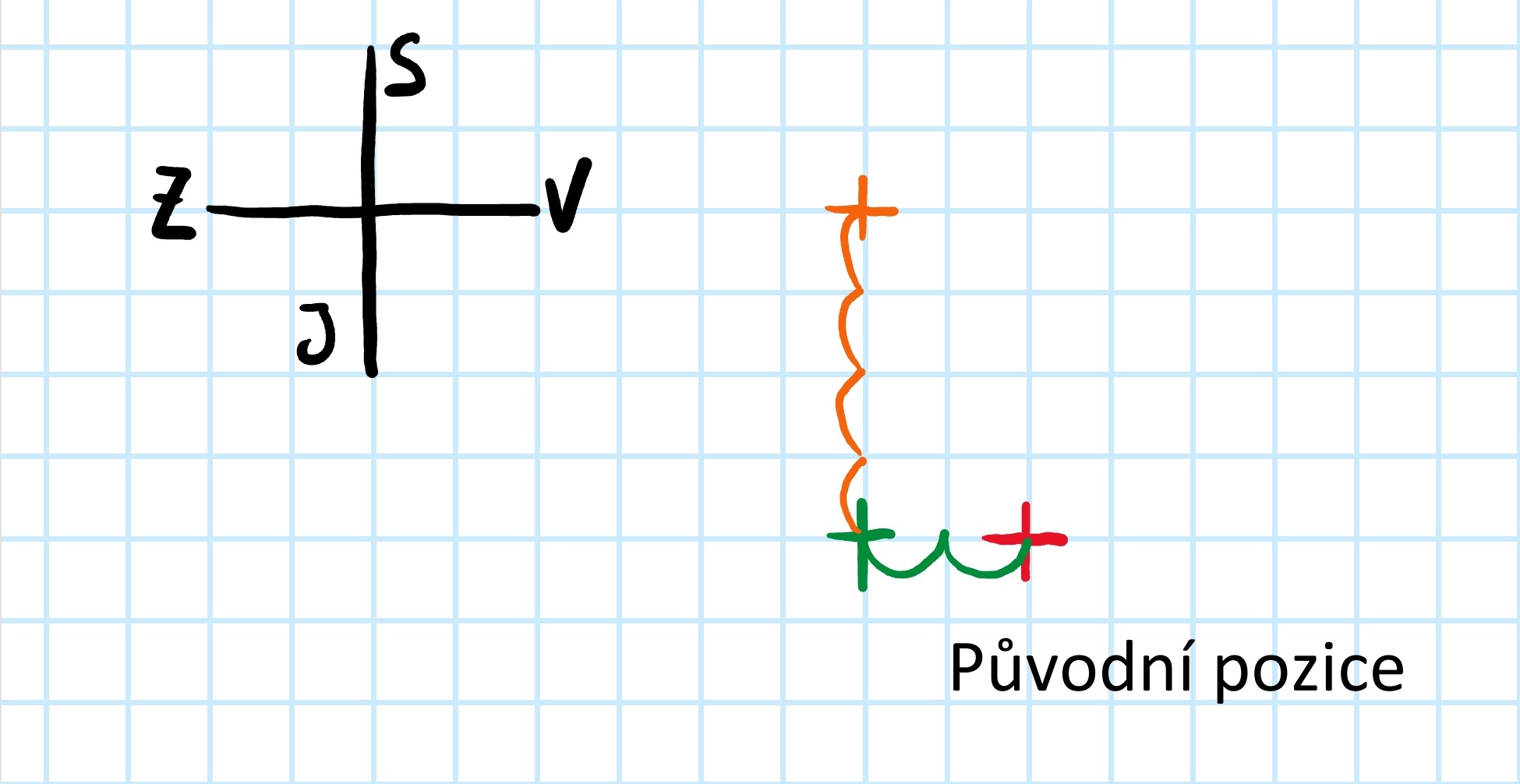
Nápověda 6
Poslední posun odpovídá 5 metrům na východ, tedy se posuneme o 5 čtverců vpravo. Konečně je keř na finální pozici.
V náčrtku je posun znázorněn fialovými obloučky, finální pozice keře fialovým křížkem.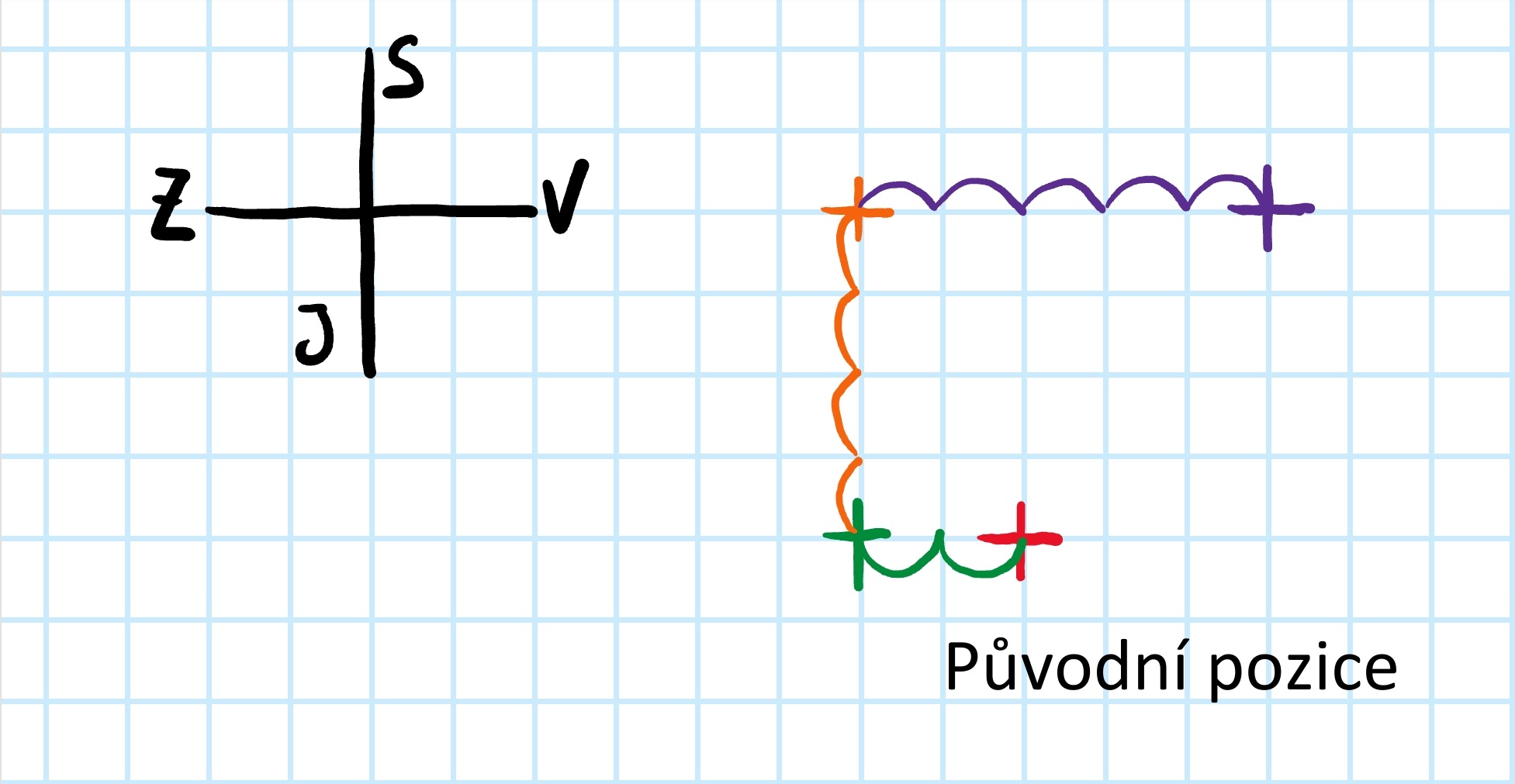
Nápověda 7
Spojte body, které znázorňují původní a finální pozici keře. Víte, jak tuto vzdálenost spočítat?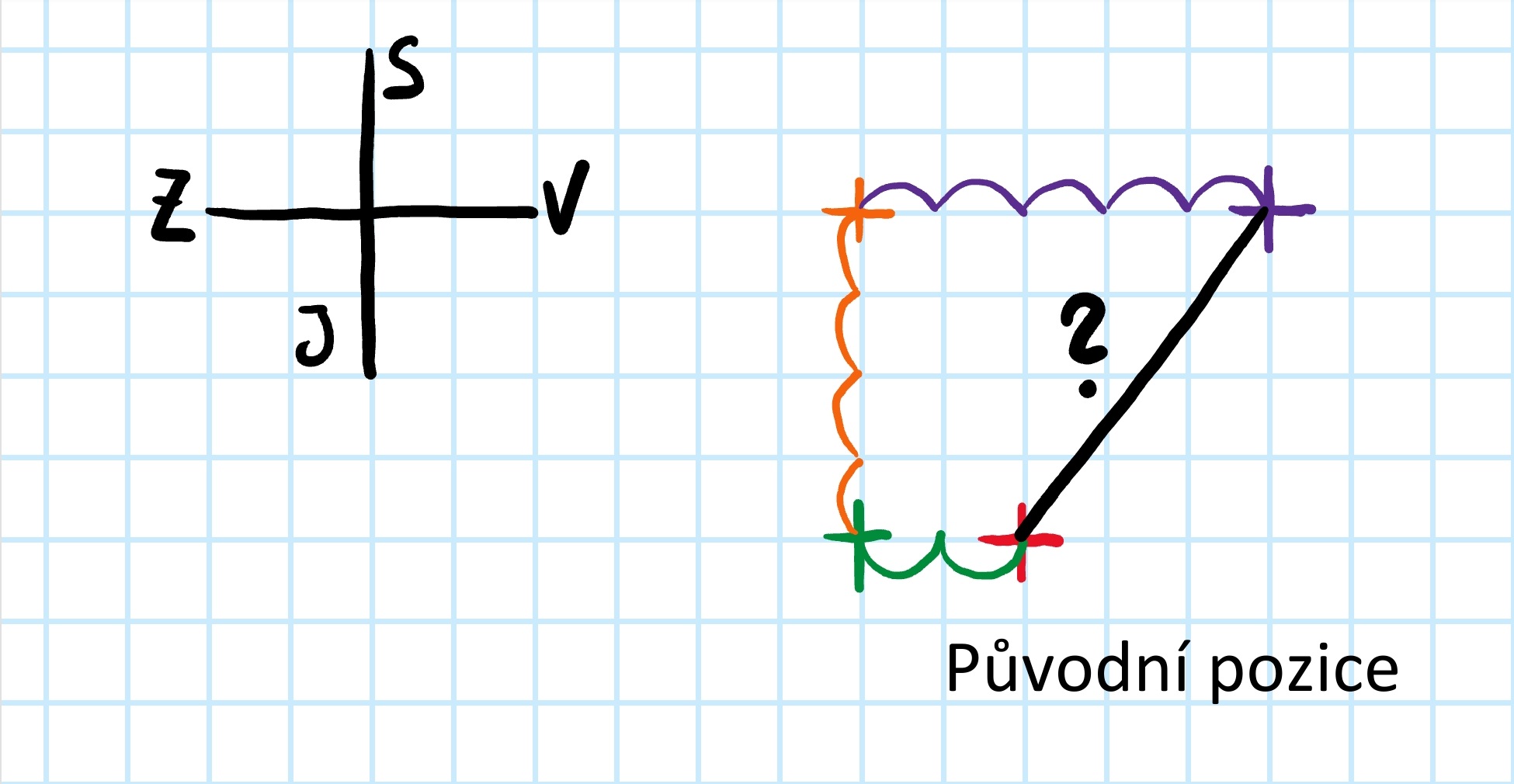
Nápověda 8
Najděte ve vaší mřížce takový pravoúhlý trojúhelník, pro který platí, že spojnice původní a finální pozice keře je jeho přepona. Pozice keřů jsou dva z jeho vrcholů. Díky mřížce můžete snadno zjistit délku jeho odvěsen. Teď už stačí spočítat délku přepony pomocí Pythagorovy věty.
V náčrtku jsme odvěsny trojúhelníku vyznačily modře.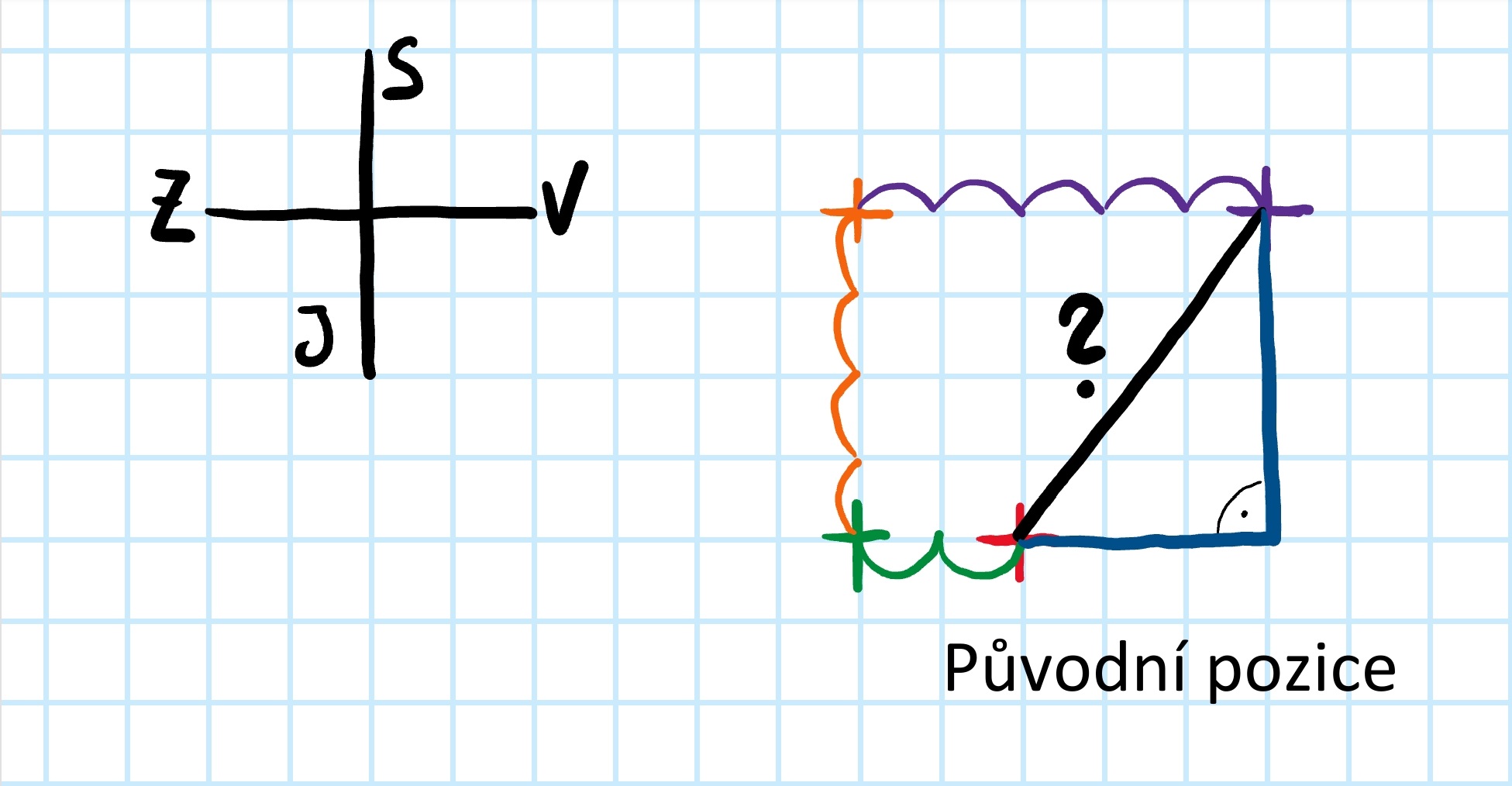
Nápověda 9
Pythagorova věta platí v pravoúhlých trojúhelnících, k výpočtu se využívá vzorec c2 = a2 + b2, kde c značí přeponu a zbylé strany jsou odvěsny. Strana a má v našem případě délku 3 m, strana b měří 4 m.
Jak jsme na délku přišli? Díky mřížce jsme spočítali, jak jsou strany dlouhé. Strana a zabírá 3 čtverečky, strana b zabírá 4 čtverečky.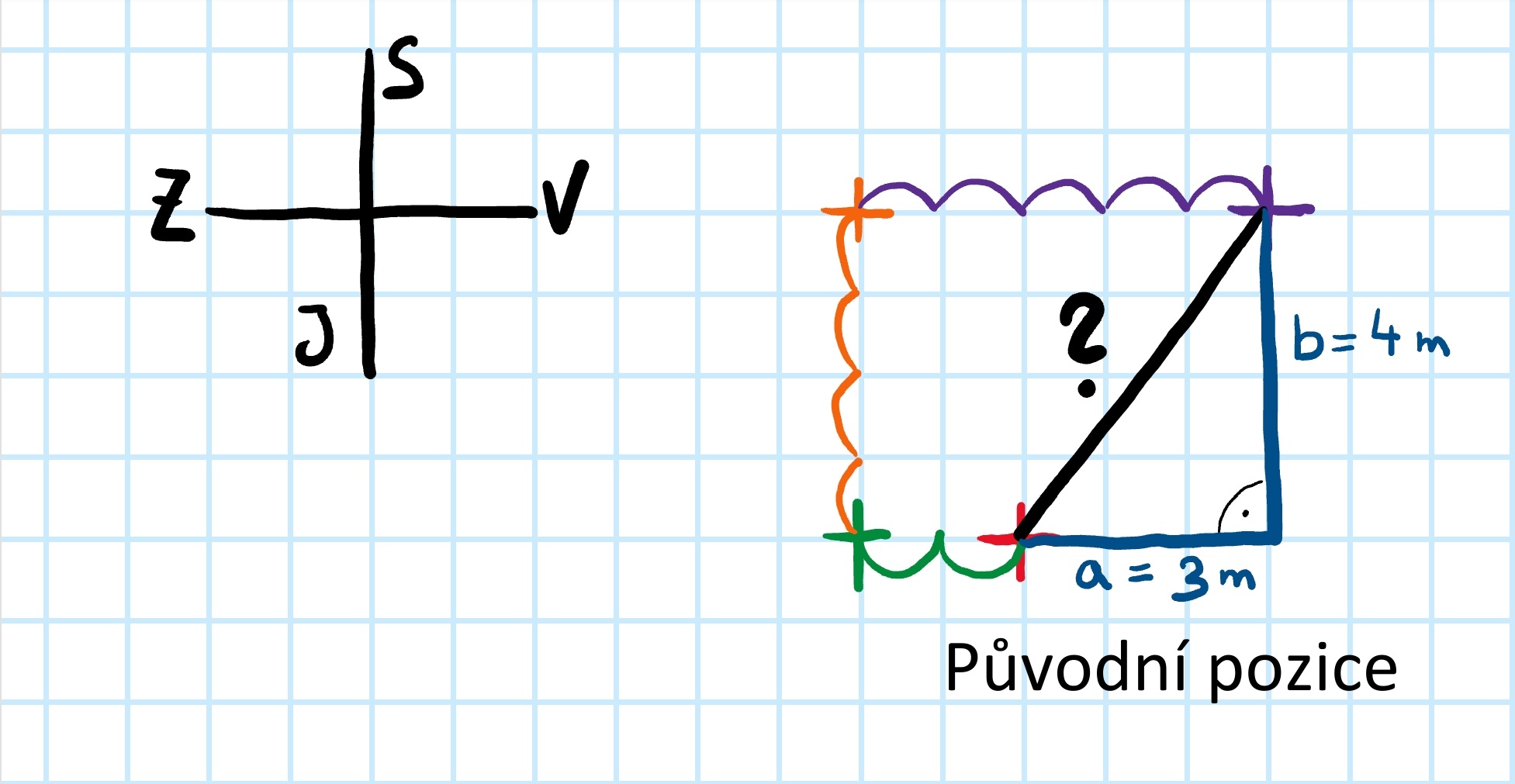
Nápověda 10
Po dosazení do vzorce postupně vychází:
c2 = 32 + 42
c2 = 9 + 14
c2 = 25.
Po odmocnění nám vyjde délka přepony c = 5 m, což je vzdálenost původního místa keře od jeho finální pozice.
Správná odpověď
Keř je nyní zasazený 5 m od původního místa.
Tato úloha kombinuje numerickou matematiku s prostorovou představivosti. Gratulujeme k úspěšnému vyřešení! Teď už jen zbývá poslední otázka: Myslíte, že růže své nebezpečné putování po zahradě přežily bez úhony? 🙂
Foto: Vygenerováno pomocí AI.
Kvízů není nikdy dost! Procvičte svou hlavičku řešením různých hádanek a dalších hříček, které najdete v naší rubrice Kvízy. A pokud místo řešení kvúzů radši čtete zajímavé fakty, tak by vás mohl zaujmout článek o souvislosti nepořádku na pracovním stole a kreativity.